Integrálok

Feladtok integrálszámításból

Előfordulhat, hogy a feladatok olyan integrálra vezetnek, amelyeket nem lehet anlítikusan meghatározni. Elegendő ekkor csak az integrált felírni.

1. Feladat
   A Hubble-teleszkóp parabolatükréből űrszeméttel való ütközés miatt kitörött egy kis darab. A pótláshoz szükséges a tükördarab mögötti szigetelőanyag, az ezüsttel bevont üveg pótlása és persze ragasztóra is szükség lesz. Számoljuk ki ezek mennyiségét!

   Az alábbi feladatnál csak az integrálok felírása a feladat, a apontos határokkal!

   Legyen adott az \(S\) felület: \[z=a(x^2+y^2)\] Az \(S\) tartóját az \(x-y\) síkban legyen \(T\). A \(T\) háromszöget határoló egyenesek egyenleteit lásd az ábra mellett:

   0.5

   0.5 \[\begin{aligned} y&=x\cr y&=-x\cr y&=2-2x\end{aligned}\]

   • Paraméterezzük fel az \(T\) háromszöget \(s,t\) változókkal, ha \(s=x-y\), illetve \(t=x+y\)! (Adjuk meg a határokat!)

   • Számoljuk ki \(T\) felületét!

   • Számoljuk ki a \(S\) parabola alatti térrész térfogatát! (Miért 1 a Jakobi-determináns? Mik az integrálási határok?)

   • Mekkora \(S\) felülete?

   • Mekkora \(S\) határának hossza?

2. Feladat

   a.)

   Egy \(R\) sugarú hengerre \(d\) átmérőjű huzalból \(l\) hosszúságút tekerünk szorosan egymás mellé. Milyen hosszan fedhetjük be a henger felületét a huzallal?

   Segítség: A henger felületére feltekeredő drót egyenlete: \[\begin{aligned} x &= R \cos(t) \\ y &= R \sin(t) \\ z &= at, \end{aligned}\] ahol az \(a\) paramétert úgy kell megválasztani, hogy egy menet feltekerése esetén a \(z\) változő éppen egy huzal vastagságnyit emelkedjen.

   b.)

    
   

   0.4

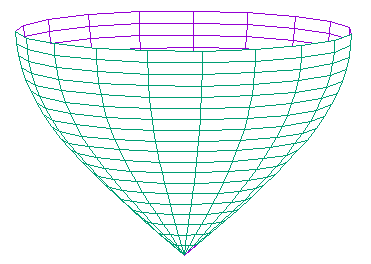
   0.45 Az szomszéd ábrán látható felületre feltekeredő fonal egyenletét a következőképpen adhatjuk meg: \[\begin{aligned} x &= \sin(t)\cos(t) \\ y &= \sin(t)\sin(t) \\ z &= at \end{aligned}\] Hogyan válasszuk meg az \(a\) paramétert, ha egy \(l\) hosszúságú fonállal, amely a az alakzat csúcsáról indul fel akarunk érni a peremére?

3. Feladat
   

   0.50 Az ábrán látható nyílt felületet a következőképpen parametrizálhatjuk: \[\begin{aligned} x &= \sin(u)\cos(v) \\ y &= \sin(u)\sin(v) & , & 0 \leq u \leq 3/4 \pi & , & 0 \leq v \leq 2\pi \\ z &= au \end{aligned}\] Számítsuk ki a fluxust, ha a felület a következő erőtérben helyezkedik el: \[\mathbf{E} = \left ( \begin{array}{c} 0 \\ 0 \\ E_0 e^{-(x^2 + y^2)} \end{array} \right ) \;.\] Mekkora az erőtér divergenciája? Mekkora lenne a fluxus, ha zárt felületre számítanánk ki? (Gauss tétel) Érdemes polár koordináta rendszerben dolgozni!

   0.35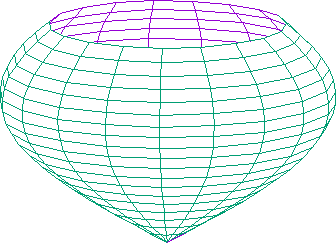

4. Feladat
   Legyen adott a \(z=b-a(x^2+y^2)\) egyenletű paraboloid

   1. Paraméterezze hengerkoordináta rendszerben!

   2. Ha \(z\geq0\) mekkora a paraboloid térfogata?

   3. Mekkora a paraboloid felszíne?

   4. Mekkora a paraboloid fluxusa a \({\mathbf{F}}=(x,y,z)\) vektormezővel?

5. Feladat
   Egy \(alpha\) nyításszögű kúp felületére egy fonalat tekerünk fel \(h\) menetemelkedéssel. Milyen hosszú fonalra lesz szükségünk \(n\) menetszámhoz? Mekkora lesz a fonal helyzeti energiája, ha \(1m\) fonal súlya \(10g\)?

6. Feladat
   Egy R sugarú gömb felszinén számítsuk ki egy a gömb középpontjától \(z_0\) távolságra helyezett pozitív ponttöltés elektromos terének a fluxusát! Dolgozzunk henger koordináta rendszerben!

7. Feladat
   Egy ellipszoidnak a következő az egyenlete: \[x^2 + 5y^2 + 4zy + 2z^2 = 1\] Határozzuk meg az ellipszoid és az \(xy\) sík metszetének a területét!

8. Feladat
   Egy kúp köré tekeredő drótot a következőképpan parametrizálunk: \[\mathbf{r} = \left ( \begin{array}{c} b\varphi \cos(\varphi) \\ b\varphi\sin(\varphi) \\ a\varphi \end{array} \right )\]

   a.) Írjuk fel az \(\mathbf{r}(\varphi)\) vektort henger koordinátákban és a henger koordináta rendszerben használatos \(\mathbf{e}_\rho\), \(\mathbf{e}_\varphi\), \(\mathbf{e}_z\) egységvektorok felhasználásával!

   b.)

   Milyen hosszú drótra lesz szükségünk, ha \(n\) menetet szeretnék a kúpra tekerni?

   c.)

   Ha a drótot nem a kúp csúcsában, hanem \(z_0\) magasságban kezdjük feltekerni, akkor mekkora lesz a mágneses indukció \(z\) komponense a kúp csúcsában, ha \(I\) áram folyik a tekercsben? Alkalmazzuk a Biot-Savart törvényt: \[\mathbf{B} = -\frac{\mu_0}{4\pi}I\int \frac{d\mathbf{r}\times \mathbf{r}}{r^3}\]

9. Feladat
   Egy szolenoidban a tekercset a következőképpen parametrizálhatjuk: \[\mathbf{r} = \left ( \begin{array}{c} r\cos(\varphi) \\ r\sin(\varphi) \\ a\varphi \end{array} \right ) = r\mathbf{e}_\rho + a\varphi\mathbf{e}_z \;,\] ahol \(r\) a tekercs sugara, az \(a\) paraméter pedig a menetemelkedést határozza meg. Mutassik meg, hogy a mágneses térerősség a henger tengelyével párhuzamos komponense a tengelye mentén a henger közepén lesz a legnagyobb!

10. Feladat
    Egy testet felületét a következőképpen parametrizálhatjuk: \[\mathbf{r}(u,v) = \left ( \begin{array}{c} (1+\cos(u))\cos(v) \\ (1+\cos(u))\sin(v) \\ u \end{array} \right ) \qquad u \in [-\pi,\pi]\;, \quad v \in [0,2\pi]\] Mekkora lesz a térfogata? Mutassuk meg hogy a test térfogatát a következő felületi integrálokkal is megadhatjuk: \[\int \frac{1}{3}\mathbf{r}d\mathbf{A} = \int z\mathbf{e}_zd\mathbf{A} = \int\frac{1}{2}\rho\mathbf{e}_\rho d\mathbf{A}\]