Egy \(m\) tömegű, \(R\) ellenállású fém rúd egy hosszú sínen mozoghat sűrlódás nélkül a sín síkjára merőleges homogén mágneses térben. A sín ellenállása elhanyagolható. A sínpár egyik végére időben változó \(V(t)\) feszültséget kapcsolunk. Hogyan fog mozogni a sínen a rúd?
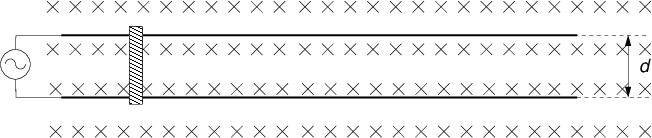
Legyen a sínpárra kapcsolt feszültség \(V(t) = V_0\sin(\omega t)\) alakú. A Faraday törvény értelmében az indukált feszültség: \(\displaystyle V = -\frac{d \Phi}{dt}\), ahol \(\Phi\) mágneses tér fluxusát jelőli. A mi esetünkben: \(\Phi = Bxd\), ahol \(x\) a rúd elmozdulását jelöli. Ekkor az indukélt feszültség \(V = Bdv\), ahol \(v = \dot{x}\), a rúd sebessége. A rúdra ható erő a Lorentz erő: \(\mathbf{F} = I\,\mathbf{l}\times \mathbf{B}\) melynek nagysága az esetünkben \(F = IBd\). Írjuk fel a hurok törvényt és a Newton egyenletet a rúdra: \[\begin{aligned} V_0\sin(\omega t) - Bdv = IR &,& IBd = m\dot{v} \;. \end{aligned}\] Vonjuk össze a két egyenletet: \[\frac{mR}{Bd}\dot{v} + Bdv = V_0\sin(\omega t) \;,\] \[\dot{v} + \frac{B^2d^2}{mR}v = \frac{V_0Bd}{mR}\sin(\omega t) \;.\] Vezessük be az \(\displaystyle\alpha = \frac{B^2d^2}{mR}\) és \(\displaystyle\beta=\frac{V_0Bd}{mR}\) változókat. Az új változókkal kapott alakot vessük össze az előadáson tanult formával: \[\begin{aligned} \dot{v} + \alpha v = \beta \sin(\omega t) & \ & \leftrightarrow & \ & \dot{v} + p(t) v = q(t) \end{aligned}\]
Az ilyen típusú k.d.e esetén kövessük a megoldási sémát: \[\begin{aligned} u(t) = e^{\int p(t)dt} &,& u(t) = e^{\alpha t} \\ v(t) = \frac{1}{u}\int u(t)q(t)dt + \frac{C}{u} &,& v(t) = e^{-\alpha t} \int \beta e^{\alpha t}\sin(\omega t)dt + Ce^{-\alpha t} \end{aligned}\]
\[\int e^{\alpha t}\sin(\omega t)dt = \frac{1}{2i} \int \left (e^{(\alpha +i\omega)t} - e^{(\alpha -i\omega)t}\right )dt = e^{\alpha t} \left (\frac{\alpha}{\alpha^2 + \omega ^2}\sin(\omega t) - \frac{\omega}{\alpha^2 + \omega ^2}\cos(\omega t) \right )\] Tehát a megoldás: \[v(t) = \frac{\alpha\beta}{\alpha^2 + \omega ^2}\sin(\omega t) - \frac{\omega\beta}{\alpha^2 + \omega ^2}\cos(\omega t) + Ce^{-\alpha t}\]
Adjuk meg a következő differenciálegyenlet általános megoldását: \[\begin{aligned} &\mbox{a.)}& y^\prime = \ln(x)y \\ &\mbox{b.)}& y^\prime-\frac{2y}{x} = 0 \\ \end{aligned}\]
An integrating factor is any expression that a differential equation is multiplied by to facilitate integration and is not restricted to first order linear equations. For example, the nonlinear second order equation
\[\frac{d^2 y}{d t^2} = A y^{2/3}\]
admits \(\tfrac{d y}{d t}\) as an integrating factor:
\[\frac{d^2 y}{d t^2} \frac{d y}{d t} = A y^{2/3} \frac{d y}{d t}.\]
To integrate, note that both sides of the equation may be expressed as derivatives by going backwards with the [[chain rule]]:
\[\frac{d}{d t}\left(\frac 1 2 \left(\frac{d y}{d t}\right)^2\right) = \frac{d}{d t}\left(A \frac 3 5 y^{5/3}\right).\]
Therefore
\[\left(\frac{d y}{d t}\right)^2 = \frac{6 A}{5} y^{5/3} + C_0.\]
This form may be more useful, depending on application. Performing a separation of variables will give:
\[\int \frac{d y}{\sqrt{\frac{6 A}{5} y^{5/3} + C_0}} = t + C_1;\]
this is an implicit solution which involves a nonelementary integral. Though likely too obscure to be useful, this is a general solution. Also, because the previous equation is first order, it could be used for numeric solution in favor of the original equation.
Határozzuk meg a következő kezdetiérték probléma megoldását: \[\begin{aligned}
t\dot{y} + 2y = t^2 -t +1 & , & y(1) = \frac{1}{2}
\end{aligned}\] (Dowkins könyv 37. oldal)
Vegyük észre, hogy az egyenlet átírható a \[\frac{d}{dt}(t^2y) = t^3 - t^2 + t\] alakba.
Határozzuk meg a következő kezdetiérték probléma megoldását (Dowkins: 44. old.): \[\begin{aligned} \dot{y} = \frac{3x^2 +4x -4}{2y-4} & , & y(1) = 3 \end{aligned}\]
Bolygómozgás
Egy rendszer energiáját 2D polárkoordinátákban a következőképpen tudjuk megadni: \[E = \frac{1}{2} \frac{l^2}{mr^4}\left( \frac{d r}{d\varphi}\right)^2 + \frac{1}{2}\frac{l^2}{mr^2} -\frac{\alpha}{r} \;.\] Határozzuk meg a rendszer \(r(\varphi)\) pályáját!