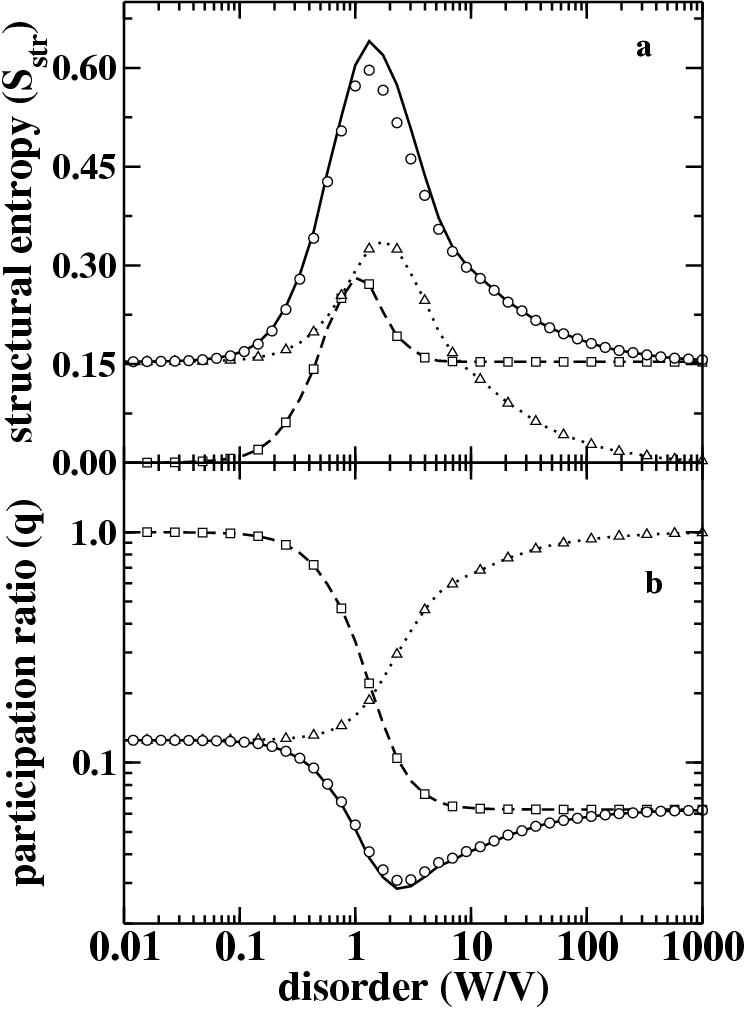
We discuss some properties of the generalized entropies, called Rényi entropies and their application to the case of continuous distributions. In particular it is shown that these measures of complexity can be divergent, however, their differences are free from these divergences thus enabling them to be good candidates for the description of the extension and the shape of continuous distributions. We apply this formalism to the projection of wave functions onto the coherent state basis, i.e. to the Husimi representation. We also show how the localization properties of the Husimi distribution on average can be reconstructed from its marginal distributions that are calculated in position and momentum space in the case when the phase space has no structure, i.e. no classical limit can be defined. Numerical simulations on a one dimensional disordered system corroborate our expectations.
