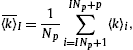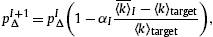Copyright © 2008 Elsevier B.V. All rights reserved.
Model of community emergence in weighted social networks
J.M. Kumpulaa,  ,
,  , J.-P. Onnelaa, b, J. Saramäkia, J. Kertésza, c and K. Kaskia
, J.-P. Onnelaa, b, J. Saramäkia, J. Kertésza, c and K. Kaskia
aDepartment of Biomedical Engineering and Computational Science, Helsinki University of Technology, P.O. Box 9203, FIN-02015 HUT, Finland
bPhysics Department, Clarendon Laboratory, Oxford University, Oxford OX1 3PU, UK
cInstitute of Physics, Budapest University of Technology and Economics, Budapest, Hungary
Received 15 September 2008;
Abstract
Over the years network theory has proven to be rapidly expanding methodology to investigate various complex systems and it has turned out to give quite unparalleled insight to their structure, function, and response through data analysis, modeling, and simulation. For social systems in particular the network approach has empirically revealed a modular structure due to interplay between the network topology and link weights between network nodes or individuals. This inspired us to develop a simple network model that could catch some salient features of mesoscopic community and macroscopic topology formation during network evolution. Our model is based on two fundamental mechanisms of network sociology for individuals to find new friends, namely cyclic closure and focal closure, which are mimicked by local search-link-reinforcement and random global attachment mechanisms, respectively. In addition we included to the model a node deletion mechanism by removing all its links simultaneously, which corresponds for an individual to depart from the network. Here we describe in detail the implementation of our model algorithm, which was found to be computationally efficient and produce many empirically observed features of large-scale social networks. Thus this model opens a new perspective for studying such collective social phenomena as spreading, structure formation, and evolutionary processes.
Keywords: Communities; Weighted network; Social network
PACS classification codes: 89.75.Hc; 89.65.-s; 89.75.Fb
Article Outline
- 1. Introduction
- 2. The model
- 2.1. Microscopic rules
- 2.2. Algorithmic implementation
- 2.3. Simulation parameters and initial conditions
- 3. Results
- 3.1. Scaling of the algorithm
- 3.2. Basic distributions
- 3.3. Network community structure by clique percolation
- 3.4. Weight-topology correlations
- 4. Conclusions
- Acknowledgements
- References
1. Introduction
Various complex systems, from genetic transcriptions to human societies, have been approached from the perspective of network theory, turning out to contribute significantly to the understanding of their structure, function, and response [1] and [2]. In case of human social systems, this approach was first adopted by social scientists [3] and [4] studying fairly small data sets collected from, e.g., questionnaires and then by physicists [5], [6], [7], [8] and [9] focusing on large-scale data sets collected from, e.g., Internet, emails etc., both giving insight into social network structure with one-to-one interactions. In the social sciences the network paradigm is that social life consists of the flow and exchange of norms, values, ideas, and other social and cultural resources channeled through a network [10]. By studying large-scale social networks we can get insight into collective social phenomena such as diffusion and spreading processes (epidemics), opinion formation, and evolution of language, etc. In order to do so we ask (i) how are large scale social networks organized and (ii) can they be modeled with a simple model.Answering the first question has traditionally been based on the analysis of data from questionnaires typically among N=102–103 individuals with a wide scope social interactions but with limited resolution in quantifying unambiguously the strength of interaction between a pair of individuals. In the new approach data is obtained from electronic records of interactions between typically of N=106 individuals with a narrower scope of social interactions but as such accurately quantifiable through measurements. We have demonstrated the success of the new approach by studying social interaction network constructed from a very large data set of mobile phone communication logs [11]. Apart from its global structure this network shows local structure due to link weights or tie strengths, such that the network was found to be modular in terms of communities with dense and stronger internal links connected sparsely with weaker external links. This network shows high degree clustering and assortative mixing demonstrating that high degree nodes in the network are connected to other high degree nodes. Perhaps the most noteworthy finding of this empirical study, however, is that the network verifies the “strength of the weak ties” hypothesis by Granovetter stating: Tie strength between two individuals increases with the overlap of their friendship circles. Moreover, the weak and strong ties have different roles such that the weak ties maintain the global integrity of the network while strong ties maintain the communities. In addition the structural properties of the network at meso-scale were found to play an important role in its functional properties, e.g., diffusion of information.
Inspired by these empirical findings from a social network the latter question can be rephrased as an aim to design a simple microscopic model to reproduce similar structural properties and then using it to simulate dynamical processes. The fact that the empirical network is structured as modules or communities raises the question “How do the communities emerge during the growth of the network”. On the other hand the fact that the links of the network are weighted raises the question “how do they influence the formation of mesoscopic communities and macroscopic network topology”. Then the empirical verification of Granovetter's hypothesis links these two questions as “how should we take into account the weight-topology correlation”. Thus we aim to build a model, in which individual-level microscopic mechanisms translate to forming on one hand mesoscopic communities and on the other hand the whole system at the macroscopic level. In this network sociology comes to help in identifying two fundamental mechanisms for network tie formation leading to network evolution: (i) cyclic closure forming ties at short range with one's network neighbors, and (ii) focal closure forming ties independently of the range through shared activities [12]. Here we adopt a simple scenario that new ties are created preferably through strong ties with every interaction making them even stronger, mimicking people getting acquaintances with local and global search mechanisms dependent on link weights unlike the mechanisms proposed by Marsili et al. [13] and Davidsen et al. [14].
In this paper we give a detailed account of our model on social community formation [15], in terms of describing the modelling methodology and algorithms used. Although our perspective aims to be sociologically relevant and to corroborate some empirical findings we believe that our model serves as a quite general paradigm for community formation in other contexts as well. This paper is organized such that we first describe the model with account to the microscopic mechanisms, their algorithmic implementation, and parameter and initial condition settings. Then we discuss the results by describing the scaling of our algorithm, basic distributions of the formed networks, community detection in them, and their weight-topology correlations. Finally we draw conclusions.
2. The model
As described above we have built the model algorithm to mimic the network tie formation processes identified by sociology. While the actual processes taking place in the formation of social relations are undoubtedly very complex, sociology research has shown that getting new acquaintances consist of mainly two processes, which in our model are simplified to the mechanisms of local search and random (global) attachment. In sociology the effect of link weight is very complicated to investigate empirically but it is reasonable to assume that people interact mostly through their “strong friendships” such that each interaction makes this connection even stronger. In reality it is also possible that some friendships disappear corresponding to deletion of a link between two nodes. However, this process is often so slow that it is difficult to observe from available data due to it being restricted to rather narrow time windows. In our model the number of links is reduced by deletion of a node and all the links connected to it. This could correspond to a situation, in which the individual having belonged to the network for a while goes out of its scope (e.g., in case of mobile communication changing the carrier).
2.1. Microscopic rules
The
microscopic rules of our model consist of two processes that create
links into a network and one process that removes them. The first
process of link formation is local search for new acquaintances (LA
process), which is modeled by two steps of a weighted self-avoiding
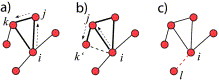
random-walk, see Fig. 1(a), (b). In the first step, node νi chooses one of its neighbors, νj, with probability wij/si where, wij is the link weight connecting nodes νi and νj, and si=∑jwij. In the second step the search continues similarly to a neighbor of νj (but avoiding νi). The visited links are reinforced by a small amount δ. If the two-step search ends at a node that is not a neighbor of the start node, this link is established with probability pΔ to a unit weight w=1. Otherwise, the existing link is reinforced by δ. In addition to the local search each node can establish a random link with probability pr at each time step (GA process), see Fig. 1(c). Also, if a node does not have links, it creates one random link with a unit weight w=1. Finally, at each time step a node is deleted (ND process) with probability pd,
which is the only process that decreases the number of links in the
network. Note that the removed node gets replaced by a new node at next
time step, which keeps the network size N constant. The random deletion of nodes leads to exponential distribution for node and link lifetimes, averages of which are ![]() and
and  τw
τw =(2pd)−1, respectively.
=(2pd)−1, respectively.
 | Full-size image (10K) |
Fig. 1. The microscopic rules of the model consist of two processes. The first process of tie formation is local search (cf. cyclic closure). (a) A weighted local search starts from i and proceeds first to j and then to k, which is a neighbor of i. (b) The local search from i ends to k′, which is not a neighbor of i. In this case a link wik′ of unit weight (w = 1) is established with probability pΔ. The second process for tie formation is random link creation (focal closure). (c) Node i creates a random link to a random node l with probability pr. In cases (a) and (b) the weights of involved links are increased by the amount δ.
2.2. Algorithmic implementation
In most cases our model with microscopic rules described above produces very sparse networks, i.e., the average degree is much less than the network size, thus making their storage as full matrixes very inefficient from computational point of view. Instead we have implemented the model by storing the network Γ as a linear-probing hash-table [16], which guarantees small memory consumption, constant time retrieval of network nodes and links, and efficient looping over the neighbors of each node. At the beginning of the simulation the model network Γ is empty, i.e., it contains N nodes but no links. The simulation proceeds in time such that at each time step the nodes perform the LA and GA processes on network Γ. However, Γ is kept unchanged during the time step and a temporary network Γ* is used to store the changes resulting from LA and GA processes such that weight increase of existing links and new links are added to Γ*. At the end of each time step the network Γ is updated by looping over the links of Γ* and copying the weight increases and new links to Γ, after which all links are removed from Γ*.
As mentioned earlier, the number of links is reduced by removing nodes randomly from the network and correspondingly adding nodes without links to keep the network size constant. In practise, the node removal process is handled as follows: when a node is chosen to be removed, it is not actually deleted from the network but all links connected to it are removed. At next time step this empty node will join the network by introduction of a random link as described in Section 2.1.
2.3. Simulation parameters and initial conditions
The simulations start from an empty network of N
nodes and proceed in time such that the changes due to local searches,
random attachments, and node deletions are updated at the end of each
time step. Average node lifetime  τ
τ was set to 1000 time steps and random link probability to pr=1×10−3
corresponding to adding on average 2 random links for each node during
average node lifetime. The following results were obtained after
running the simulations for 25×103 time steps, which is long enough for all the statistics of the model to reach a steady state.
was set to 1000 time steps and random link probability to pr=1×10−3
corresponding to adding on average 2 random links for each node during
average node lifetime. The following results were obtained after
running the simulations for 25×103 time steps, which is long enough for all the statistics of the model to reach a steady state.
The
weights enter the model dynamics through the reinforcement of visited
links, which is controlled by the “friendship reinforcement” parameter δ. When δ
is large some links start to dominate the local search process
attracting almost all searches and becoming all the time stronger. In
this case the search ends up almost always to a “familiar” node, that
is, the start and end nodes are already connected. On the other hand,
when δ=0
the local search follows all links with equal probability. Now the
search exits the neighborhood of the start node quite easily, and a new
link is then established with probability pΔ. Other parameters being fixed the average degree of the network is thus controlled by parameters δ and pΔ. In practice pΔ is adjusted for each δ such that the average degree  k
k remains constant, here we use
remains constant, here we use  k
k =15 unless otherwise mentioned. Keeping
=15 unless otherwise mentioned. Keeping  k
k constant allows easy comparison of networks with different δ
and ensures that differences in the network structure result solely
from the reorganization of the links. Below we present a simple
algorithm for automatically adjusting pΔ for each value of δ and average target degree
constant allows easy comparison of networks with different δ
and ensures that differences in the network structure result solely
from the reorganization of the links. Below we present a simple
algorithm for automatically adjusting pΔ for each value of δ and average target degree  k
k target.
target.
First, we note that  k
k is a monotonically increasing function of pΔ when other parameters are kept constant. Second, the value of pΔ
can be adjusted during a simulation provided that one waits
sufficiently long time after each adjustment such that the network
structure has time to adapt to the new situation. Third, even for
constant pΔ there are random fluctuations in the value of
is a monotonically increasing function of pΔ when other parameters are kept constant. Second, the value of pΔ
can be adjusted during a simulation provided that one waits
sufficiently long time after each adjustment such that the network
structure has time to adapt to the new situation. Third, even for
constant pΔ there are random fluctuations in the value of  k
k and therefore one should not be too avid to change pΔ if
and therefore one should not be too avid to change pΔ if  k
k deviates from
deviates from  k
k target. Now, suppose we have decided
target. Now, suppose we have decided  k
k target, fixed δ and pr, and initiated the simulation with an initial guess
target, fixed δ and pr, and initiated the simulation with an initial guess ![]() . We measure the average degree of the network at 1000 time step intervals, and denote the ith measurement by
. We measure the average degree of the network at 1000 time step intervals, and denote the ith measurement by  k
k i. The value of pΔ is adjusted after Np such measurements; here we have used Np=7. The average of Np measurements of
i. The value of pΔ is adjusted after Np such measurements; here we have used Np=7. The average of Np measurements of  k
k i is denoted by
i is denoted by
where αI=0.9αI−1 and α0=2. The optimal value for pΔ is usually obtained after 100 adjustment rounds, e.g., by setting
3. Results
3.1. Scaling of the algorithm
Before
presenting results for the formation of social networks we first
investigate the CPU-time scaling of our model algorithm. It is natural
to expect that the required CPU-time depends on the network size N, average degree  k
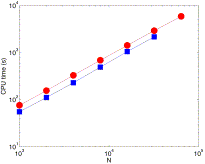
k , number of iterations, but also weakly on other network parameters. Fig. 2 shows the CPU-time as a function of network size for networks having
, number of iterations, but also weakly on other network parameters. Fig. 2 shows the CPU-time as a function of network size for networks having  k
k =10 and
=10 and  k
k =15.
The simulation runs were performed for 25000 time steps. Here it can be
seen that scaling of the CPU-time is linear for both networks, which
was expected because the algorithm uses only local processes (and the
GA process is always performed in constant time). Note also that our
algorithm could be parallelized rather easily because at each time step
the LA and GA processes for each node are independent of other
searches. However, we have not attempted this.
=15.
The simulation runs were performed for 25000 time steps. Here it can be
seen that scaling of the CPU-time is linear for both networks, which
was expected because the algorithm uses only local processes (and the
GA process is always performed in constant time). Note also that our
algorithm could be parallelized rather easily because at each time step
the LA and GA processes for each node are independent of other
searches. However, we have not attempted this.
 | Full-size image (13K) |
Fig. 2. (Color online) The scaling of CPU-time for the model algorithm as a function of network size. Networks with  k
k = 10 (pr=5
= 10 (pr=5 10−4, δ = 1, pΔ=0.044) are denoted by (○) and networks with
10−4, δ = 1, pΔ=0.044) are denoted by (○) and networks with  k
k = 15 (pr=1
= 15 (pr=1 10−3, δ = 1, pΔ=0.0719) by (□). Simulations were done on desktop computer with 3.0 GHz Pentium 4 processor.
10−3, δ = 1, pΔ=0.0719) by (□). Simulations were done on desktop computer with 3.0 GHz Pentium 4 processor.
3.2. Basic distributions
In Fig. 3 we present the basic distributions for the simulated networks with varying friendship reinforcement parameter δ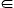 [0,1.6] and
[0,1.6] and  k
k =15. There are a number of analyses of large data bases [11], [17], [18] and [19]
that suggest at least the following common features for social
networks: (i) degree distributions are skewed, (ii) high-degree nodes
are often connected to other high-degree nodes (assortative mixing),
(iii) the average clustering coefficient
=15. There are a number of analyses of large data bases [11], [17], [18] and [19]
that suggest at least the following common features for social
networks: (i) degree distributions are skewed, (ii) high-degree nodes
are often connected to other high-degree nodes (assortative mixing),
(iii) the average clustering coefficient  c
c is high compared to random networks, and (iv) the average shortest path lengths are small (the small-world property). Fig. 3 shows also the corresponding distributions for the mobile phone call network (note that this network has
is high compared to random networks, and (iv) the average shortest path lengths are small (the small-world property). Fig. 3 shows also the corresponding distributions for the mobile phone call network (note that this network has  k
k =3.1). As can be seen, for all the studied values of δ
the properties of our model network are in agreement with features
(i)–(iii) and also with feature (iv) as the network diameter grows as logN (not shown). In this sense even δ=0
can be considered as a valid choice for modelling social networks,
since our results resemble those obtained from certain unweighted
models [13] and [14]. The effect of δ becomes important only when the community structure due to link weights is taken into account, as will be discussed next.
=3.1). As can be seen, for all the studied values of δ
the properties of our model network are in agreement with features
(i)–(iii) and also with feature (iv) as the network diameter grows as logN (not shown). In this sense even δ=0
can be considered as a valid choice for modelling social networks,
since our results resemble those obtained from certain unweighted
models [13] and [14]. The effect of δ becomes important only when the community structure due to link weights is taken into account, as will be discussed next.
 | Full-size image (32K) |
Fig. 3. (Color online) Basic distributions of model networks for several values of δ. (a) Degree distribution, (b) clustering, (c) average nearest neighbor degree knn, and (d) average link overlap as a function of cumulative link weight. Results are averaged over 50 realizations for N = 1 × 104 networks. Values for δ are 0 (□), 2 × 10−2 (*), 0.2 ( ), and 1.6 (○). Results for mobile phone call data [11] are for comparison and labeled by (+).
), and 1.6 (○). Results for mobile phone call data [11] are for comparison and labeled by (+).
3.3. Network community structure by clique percolation
The effect of δ on network structure is visualized in Fig. 4, where it is clearly seen that increasing δ
promotes the formation of communities. Moreover, strong links seem to
be confined in communities while the links between communities are
mainly weak. The topological structure of the model networks can be
studied by k-clique percolation method. This method defines the communities by adjacent cliques of k nodes, see Fig. 5(a). Here we have used a recently proposed fast algorithmic implementation for k-clique percolation [20], which scales even for very large networks. We used 4-cliques approach but similar results are obtained also for k=3 and k=5. Fig. 5(b) shows the relative largest community size Rk=4 and average community size excluding the largest community  ns
ns as a function of δ for δ
as a function of δ for δ [0,1.6]. When δ=0 the communities turn out to be quite small having at most approximately 50 nodes and the average community size is
[0,1.6]. When δ=0 the communities turn out to be quite small having at most approximately 50 nodes and the average community size is  ns
ns ≈6. Increasing δ
changes the community structure significantly. First, the 4-cliques
start to percolate through most of the network, which can be seen as a
fast increase in Rk=4, but when δ
≈6. Increasing δ
changes the community structure significantly. First, the 4-cliques
start to percolate through most of the network, which can be seen as a
fast increase in Rk=4, but when δ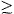 0.5 Rk=4 starts to decrease and simultaneously
0.5 Rk=4 starts to decrease and simultaneously  ns
ns increases to about 30 nodes. This means that when δ increases above
increases to about 30 nodes. This means that when δ increases above 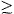 0.5
the communities start to “condense” to the initially rather homogeneous
network. The distribution of community sizes was found to be stable
after the initial lead-in time of approximately 10–20 average node life
times.
0.5
the communities start to “condense” to the initially rather homogeneous
network. The distribution of community sizes was found to be stable
after the initial lead-in time of approximately 10–20 average node life
times.
 | Full-size image (54K) |
Fig. 4. (Color online) Visualization of the effect of δ on network topology. (a) δ = 0, (b) δ = 0.1, and (c) δ = 1 ( k
k = 10 for these networks). Weak links are green and the color changes gradually to red for strong links.
= 10 for these networks). Weak links are green and the color changes gradually to red for strong links.
 | Full-size image (24K) |
Fig.
5. (a) An illustration of a 3-clique “rolling”. The 3-clique ABC
first rolls on to BCD by releasing node A. When node D is released the
3-clique rolls on CDE. Thus, nodes A, B, C, D, and E form a 3-clique
community (but not a 4-clique community since node E does not belong to
any 4-clique). (b) Largest 4-clique community size Rk=4 (○) and average community size (excluding the largest)  ns
ns (□) as a function of δ. Results are averaged over 50 realizations for size N = 1 × 104 networks.
(□) as a function of δ. Results are averaged over 50 realizations for size N = 1 × 104 networks.
3.4. Weight-topology correlations
Finally, we discuss the correlations between link weights and network topology, and the effect of δ
on them. If the strong links are confined mainly in tight communities
and the links between communities are predominantly weak, as the weak
ties hypothesis by Granovetter suggests, the network should break into
pieces easier by removing the links in ascending than in descending
order of weights. This was observed for the mobile phone call network [11] and on the basis of visual inspection of Fig. 4 one would expect also our model behave similarly when δ
is sufficiently large. To confirm this we remove links from the network
in both orders while monitoring the relative giant component size RLCC, the susceptibility ![]() , and the average clustering coefficient
, and the average clustering coefficient  c
c [5] as a function of the ration of removed links f. Here ns is the number of components of size s. The results for networks for δ
[5] as a function of the ration of removed links f. Here ns is the number of components of size s. The results for networks for δ [0,1.6] are shown in Fig. 6(a) together with the corresponding results for the mobile phone call network, in Fig. 6(b). When δ is small the giant component becomes disintegrated at the same point regardless of the link removal order and
[0,1.6] are shown in Fig. 6(a) together with the corresponding results for the mobile phone call network, in Fig. 6(b). When δ is small the giant component becomes disintegrated at the same point regardless of the link removal order and ![]() remains very small. Therefore, coupling between weights and topology
appears to be weak in this case, which is not surprising considering
the results of clique percolation. The difference between link removal
orders appear when δ
remains very small. Therefore, coupling between weights and topology
appears to be weak in this case, which is not surprising considering
the results of clique percolation. The difference between link removal
orders appear when δ 0.5. Now, when weak links are removed first, the giant component starts to disintegrate earlier and the susceptibility
0.5. Now, when weak links are removed first, the giant component starts to disintegrate earlier and the susceptibility ![]() develops a significant peak, which can be interpreted such that the
network breaks into many quite large components, i.e., communities. On
the other hand, when strong links are removed first,
develops a significant peak, which can be interpreted such that the
network breaks into many quite large components, i.e., communities. On
the other hand, when strong links are removed first, ![]() remains small for all values of δ and the giant component disintegrates always at the same point. The insets in Fig. 6(a) show the behavior of
remains small for all values of δ and the giant component disintegrates always at the same point. The insets in Fig. 6(a) show the behavior of  c
c for both link removal orders. The rapid decrease in
for both link removal orders. The rapid decrease in  c
c when removing the strong links first indicates that the strong links
locate mainly in tightly connected components, while the opposite is
true for weak links. This is corroborated also by Fig. 3(d), which shows the link overlap oij=nij/(ki+kj−2−nij), where nij is the number of common neighbors of nodes νi and νj, as a result of cumulative link weight [11]. There it is seen that also in our model the overlap increases with link weight for sufficiently large δ,
as the weak ties hypothesis suggests, thus supporting the observation
for strong links being confined in communities. Our link percolation
results are in good agreement with the corresponding results for the
mobile phone call data as can be seen in Fig. 6(b).
when removing the strong links first indicates that the strong links
locate mainly in tightly connected components, while the opposite is
true for weak links. This is corroborated also by Fig. 3(d), which shows the link overlap oij=nij/(ki+kj−2−nij), where nij is the number of common neighbors of nodes νi and νj, as a result of cumulative link weight [11]. There it is seen that also in our model the overlap increases with link weight for sufficiently large δ,
as the weak ties hypothesis suggests, thus supporting the observation
for strong links being confined in communities. Our link percolation
results are in good agreement with the corresponding results for the
mobile phone call data as can be seen in Fig. 6(b).
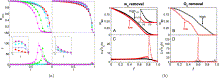 | Full-size image (57K) |
Fig.
6. (Color online) (a) Link percolation results for the model
networks. Upper panel shows the relative giant component size RLCC and the lower panel the susceptibility ![]() .
On the left: weak links are removed first; on the right: strong links
are removed first. In the inserts average clusterings are shown.
Results are averaged over 50 realizations for size N = 5 × 104 networks. Values of δ are 0 (□), 2 × 10−2 (*), 0.2 (
.
On the left: weak links are removed first; on the right: strong links
are removed first. In the inserts average clusterings are shown.
Results are averaged over 50 realizations for size N = 5 × 104 networks. Values of δ are 0 (□), 2 × 10−2 (*), 0.2 ( ), 1.0 (
), 1.0 ( ), and 1.6 (
), and 1.6 ( ). For comparison (b) link percolation results for the mobile phone call data published in [11]. Upper and lower panels and are as in the model networks (a), and descending weight removal is in black and ascending in red.
). For comparison (b) link percolation results for the mobile phone call data published in [11]. Upper and lower panels and are as in the model networks (a), and descending weight removal is in black and ascending in red.
4. Conclusions
In this paper we have introduced a simple weighted network model based on sociologically justified microscopic mechanisms to mimic mesoscopic community and macroscopic topology formation in social system. In this model the link weights are an essential part of the microscopic mechanisms establishing a coupling between network structure and interaction strengths between nodes, such that the introduction of a new link depends on the existing link weights, which are reinforced once a new link has been introduced. In addition to the local search and random attachment mechanisms that in the model correspond the cyclic closure and focal closure of network sociology, we also introduced a mechanism of random node removal with all its links simultaneously removed. The implementation of the model algorithm turned out to be computationally very efficient since the CPU-time of a simulation scales linearly with the size of the network. The simulation results show that communities emerge after nucleating from structural fluctuations but only if link weight or friendship reinforcement is sufficiently strong. In addition our model fulfills various topological and statistical properties of social networks and it exhibits weight-topology correlation complying with the Strength of Weak Tie Hypothesis by Granovetter. For this our model provides plausible mechanisms and it could in general serve as a starting point for understanding community formation in weighted networks.
Acknowledgements
J.M.K., J.-P.O., J.S. and K.K. acknowledge the Academy of Finland, the Finnish Center of Excellence program 2006–2011, proj. 213470. J.-P.O. is supported by a Wolfson College, University of Oxford, Junior Research Fellowship. J.M.K. is partly supported by the GETA graduate school. J.K. was partially supported by OTKA T049238 grant.






 E-mail Article
E-mail Article Cited By
Cited By Citation Feed
Citation Feed Export Citation
Export Citation Add to my Quick Links
Add to my Quick Links